关注不迷路，一起 From Zero To Hero !

前言

考虑一个场景：计算一个App的日活用户个数，或者统计一个页面每天访问的用户个数。这种需求都是需要对用户去重后统计数量，即统计一个集合中不重复的元素个数。在数学上把一个集合不重复元素的个数称为集合的基数（cardinality），这类问题可以称为基数统计问题。问题其实很简单，有很多常规的方法或数据结构去解决，例如：

  • 集合Set：我们可以将所有元素保存在set中，由于set本身就是去重的，最终set中的元素个数就是最终我们需要的结果值。由于我们在存储真正的数据用于去重，在数据流较小时还可以接受，但是如果数据达到百万级别甚至上亿级别时，会占用大量的内存。假设我们有1亿个不重复的元素，每个数据大小是4字节，那么使用Set至少需要 100000000*4/1024/1024≈400MB，可见内存占用量还是挺大的。

  • Bitmap：在上篇文章中，我们讨论过Bitmap的使用场景，其中就提及过二值场景，统计页面访问或者App访问的场景，也是属于二值场景。如果有1亿个用户，那么我们就需要设置一亿个bit位，用于表示每个用户的状态，那么需要占用的内存为 100000000*1/8/1024/1024≈12M。

上述两种方式都是精确的方式，但是占用内存较大。有时候我们并不需要特别精确的数据，比如对于统计页面访问量来说，1亿和一亿100万其实差别不大，这种误差是用户可以接受的。那么有没有什么算法，在可接受误差的范围内使用极少的内存来统计基数呢？答案是肯定有。在大数据计算中，有很多基数统计算法，比如：

  • Linear Counting（LC）
  • LogLog Counting（LLC）
  • HyperLogLog Counting（HLLC）
  • ······

Linear算法和位图类似，但实际使用的不多，这里不多做介绍了。本文要介绍的Redis HyperLogLog，从名字也可以看出来，Redis实现是基于HyperLogLog Counting（HLLC）算法的，HyperLogLog是LogLog算法的一个改进和优化，后面我们会一起讲解这两个算法，并学习HyperLogLog是如何在LogLog的基础上改进的。

Redis HyperLoglog最多使用12k内存来进行基数统计，并且误差可以保持在0.81%左右。接下来我们首先学习相关命令，然后再学习下原理（这种极致的统计存储，相信你和我一样，也十分好奇是怎么实现的）。

PFADD

可用版本：>= 2.8.9

时间复杂度：添加每个元素的时间复杂度为O(1)

命令格式

1

PFADD key [element [element ...]]

命令描述

  • 该命令将多个元素添加到key对应的HyperLogLog中
  • 调用命令后，HyperLogLog 内部结构可能会更新，用于表示不同元素数量（集合的基数）的估计值
  • 如果添加元素后基数估计值更新了，那么会返回1；否则返回0
  • 如果key不存在，该命令会创建一个空的HyperLogLog结构
  • 如果命令只提供了key，没有提供element参数，此时如果key已经存在，不会执行任何操作；否则会创建空的HyperLogLog

返回值

整数值：如果估计值被更新，返回1；否则返回0

示例

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# 添加元素
127.0.0.1:6379> pfadd hll a b c d e f g
(integer) 1
127.0.0.1:6379> pfcount hll
(integer) 7

# 添加重复元素
127.0.0.1:6379> pfadd hll a
(integer) 0

# 添加新元素
127.0.0.1:6379> pfadd hll h
(integer) 1
127.0.0.1:6379> pfcount hll
(integer) 8

PFCOUNT

可用版本：>= 2.8.9

时间复杂度：对于单个HyperLogLog，复杂度为 O(1)，且具有非常低的平均常数时间。当命令作用于N个HyperLogLog 时，复杂度为 O(N) ， 常数时间也比处理单个HyperLogLog 时要大得多。

命令格式

1

PFCOUNT key [key ...]

命令描述

  • 当只指定一个key时，返回HyperLogLog的近似基数；如果key不存在，返回0
  • 当指定多个key时，内部通过合并给定的多个HyperLogLog到一个临时的HyperLogLog，以此返回多个HyperLogLog并集的基数

返回值

整数值：集合基数的近似值

示例

1
2
3
4
5

# 添加元素
127.0.0.1:6379> pfadd hll a b c d e f g
(integer) 1
127.0.0.1:6379> pfcount hll
(integer) 7

PFMERGE

可用版本：>= 2.8.9

时间复杂度：O(N)，其中N为给定的key个数，但是常数时间较高

命令格式

1

PFMERGE destkey sourcekey [sourcekey ...]

命令描述

  • 将多个 sourcekey 对应的 HyperLogLog 合并（merge）到 destkey 对应的HyperLogLog，合并后的 HyperLogLog 的基数接近于所有输入 HyperLogLog 的并集
  • 如果destkey不存在，会创建一个空的HyperLogLog
  • 如果destkey已存在，命令会把destkey与所有的sourcekey一起合并，最终destkey对应的基数也包含了自身的数量

返回值

字符串：“OK”

示例

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

127.0.0.1:6379> PFADD hll1 foo bar zap a
(integer) 1
127.0.0.1:6379> PFADD hll2 a b c foo
(integer) 1
127.0.0.1:6379> PFADD hll3 d
(integer) 1

# a b c d foo bar zap 
127.0.0.1:6379> PFMERGE hll3 hll1 hll2
OK
127.0.0.1:6379>  PFCOUNT hll3
(integer) 7

原理介绍

LogLog Counting（LLC）和 HyperLogLog Counting（HLLC）都是基于伯努利实验，我们先来看下什么是伯努利实验。

伯努利实验

伯努利试验（Bernoulli experiment）是在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。我们假设该项试验独立重复地进行了n次，那么就称这一系列重复独立的随机试验为n重伯努利试验，或称为伯努利概型。单个伯努利试验是没有多大意义的，然而，当我们反复进行伯努利试验，去观察这些试验有多少是成功的，多少是失败的，事情就变得有意义了，这些累计记录包含了很多潜在的非常有用的信息。

生活中最常见的就是抛硬币了，要么是正面（1），要么是反面（0），概率都为1/2。考虑如下情形：我们一直抛硬币，直到第一次出现正面为止，我们称为一次完整的试验。可能第一次抛就出现了正面，也可能连续抛了4次才出现正面，这都算作完整的试验，我们把一次试验抛硬币的次数记为k。

我们用0表示抛到反面，用1表示抛到正面，假设我们做了N次伯努利试验，对于第次伯努利试验，所经历的抛硬币次数为$k_i$ 。在这N次伯努利试验中，最大的次数为$k_{max}$。如下图所示：

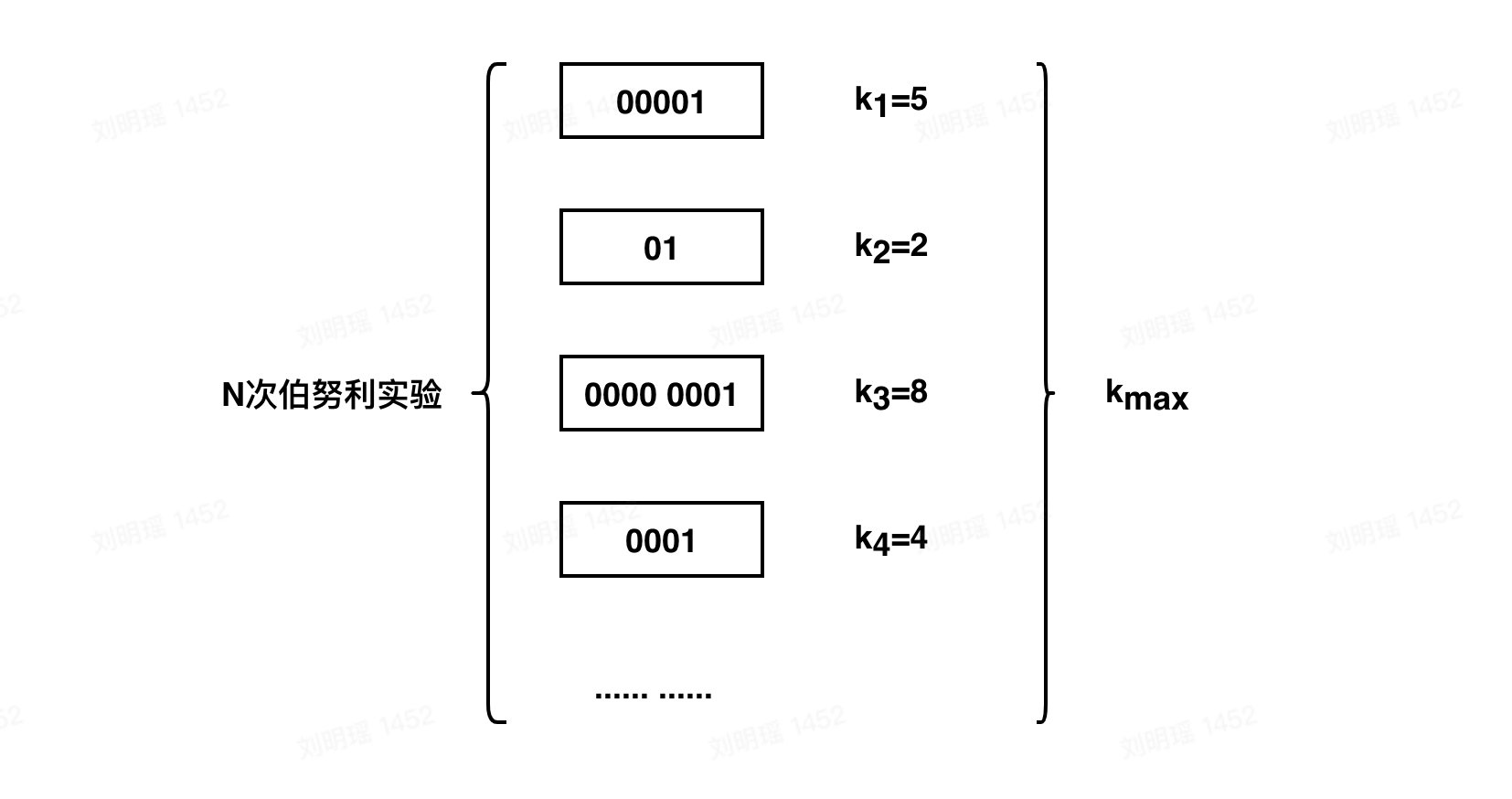
image-20210826235958224

那么如果我不告诉你 N 是多少，只告诉你$k_{max}$，你能否根据$k_{max}$去推算N呢？也就是估算我们一共做了多少次伯努利试验？这种估算在次数较少时误差较大，但是在较大数据量下，有如下结论：

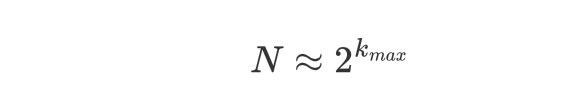
image-20210827005503166

举个栗子

简单考虑一个抛硬币序列 0001，得到这个序列的概率是多少呢？ ${1/2}^4=1/16$，那么我们反推可以得到，得到这个序列，至少需要抛硬币16次才会出现。

我们再举个例子：

（1）第1次伯努利试验，抛了2次才出现正面，$k_1=2$

（2）第2次伯努利试验，抛了3次才出现正面，$k_2=3$

（3）第3次伯努利试验，抛了2次才出现正面，$k_3=2$

（4）第4次伯努利试验，抛了1次才出现正面，$k_4=1$

因此4次实验中，$k_{max}=3$，最终我们根据$k_{max}$推断，一共做了 $2^3=8$ 次实验。这种估算在数据量较少时存在误差，但是在数据量较大时误差较小，毕竟是根据概率统计得出来的结论，有理论支持。

回到字符串上来，如果给定一批字符串，然后我们取hash值后，得到的就是01字符串，类似上面的抛硬币序列，我们从右往左找到第一个1的位置，作为$k_i$ ：

（1）011001100110011001100110，$k_1=2$

（2）010001000100010001000100，$k_2=3$

（3）011001100110011001100110，$k_3=2$

（4）010101010101010101010101，$k_4=1$

接收到这些字符串后，我们不保存字符串原值，只是更新$k_{max}$的值，最终$k_{max}=3$，我们就推断出用户一共添加了8个字符串。

分桶思想减小误差

我们在做实验的时候都知道，一次实验可能有误差，但是多次实验取平均值就可以减少误差。对于抛硬币来说，我们可以重复N次实验，然后得到N个$k_{max}$ ， 然后取平均值计算。但是和抛硬币不同，抛硬币我们每一轮的结果都是随机的，所以可以取平均减小误差，但是集合中的数据通过哈希计算得到的值是固定的，无论你计算多少轮，结果也都不会改变。那么对于集合基数的估计，如何去减小误差呢？

我们只能够从数据本身入手。一种思路就是我们把数据平均分成多份，对每一份数据进行估算，然后多份数据来进行求平均减小误差。这其实就是分桶的思想，假设数据经过处理，得到了一个32bit的二进制串，我们用低10位来表示分桶=的位置（10位最多有1024个桶），然后高22位用于模拟伯努利过程，每个桶只需要保存当前出现过的最大的 $k_{max}$ 。整个过程如下图所示：

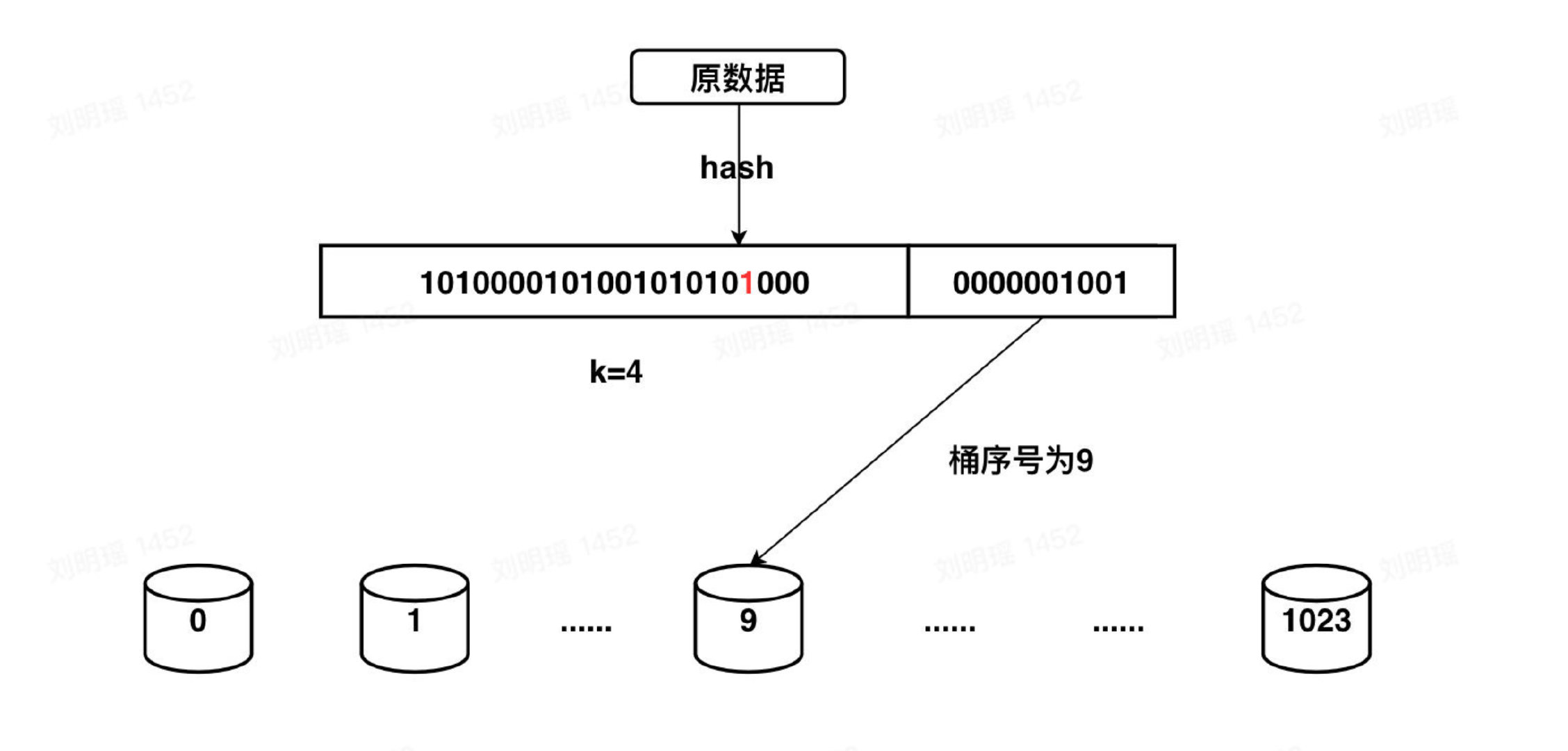
image-20210827005417945

最后我们得到1024个桶的 $k_{max}$ 值，我们可以进行取平均并估算集合的基数值。

LogLog Counting算法

LogLog Counting算法在分桶后，对这 m 个桶的 $k_{max}$ 值做一个算数平均数：

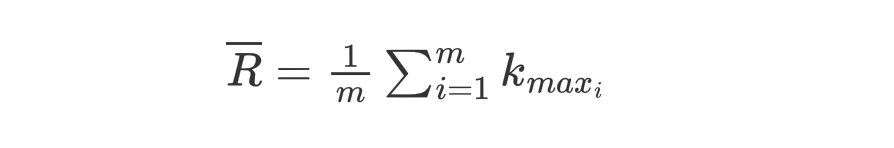
image-20210827004920631

基于 $\overline{R}$ 计算每个桶的基数，最后乘以桶数 m 和偏差修正因子 c ，就得到了整个集合的基数值：

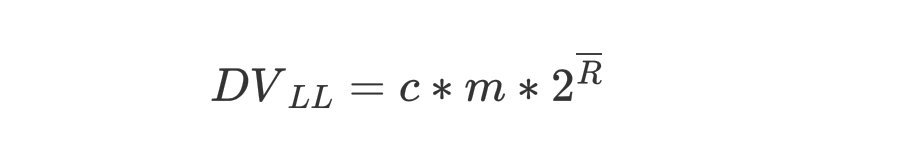
image-20210827004904349

可以看出算法的计算并不复杂。那么LLC算法占用多少空间呢？回到上面分桶的例子，我们有1024个桶，高22位去模拟伯努利试验，$k_{max}$ 的最大值也只能是22，因此每个桶只需要5bit就能保存，总共占用空间只需要 1024 * 5bit= 640B 。

HyperLogLog Counting 算法

前面的LogLog算法中我们是使用的是平均数来将每个桶的结果汇总起来，但是平均数有一个广为人知的缺点，就是容易受到大的数值的影响，一个常见的例子是，假如我的工资是1000元一个月，我老板的工资是100000元一个月，那么我和老板的平均工资就是(100000 + 1000)/2，即50500元，显然这离我的工资相差甚远，我肯定不服这个平均工资。 用调和平均数就可以解决这一问题，调和平均数的结果会倾向于集合中比较小的数，$x_1$ 到 $x_m$的调和平均数的公式如下：

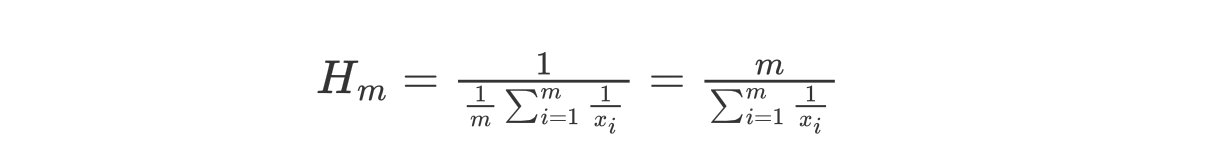
image-20210827004813451

那么对应上面的LogLog公式，HyperLogLog最终的公式为：

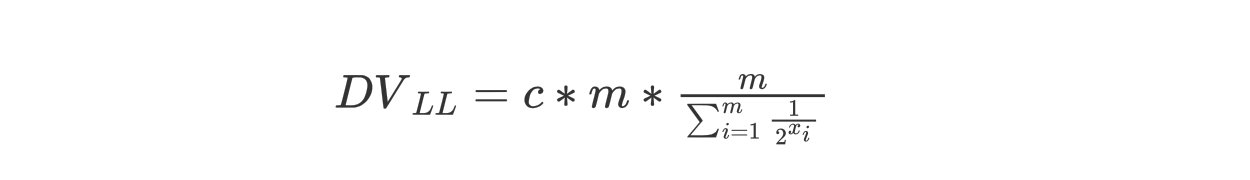
image-20210827004719775

Redis实现

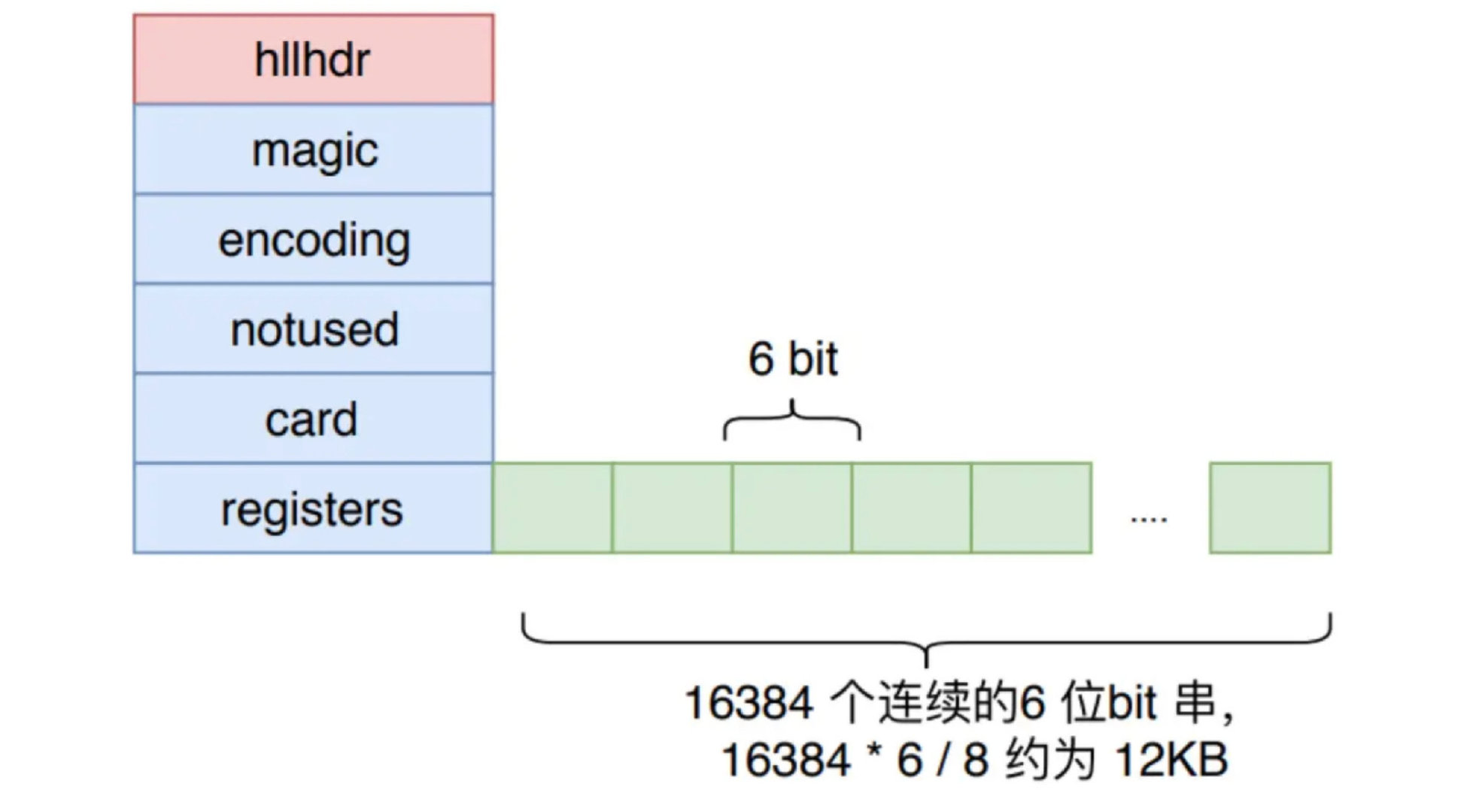
在Redis中，添加到 HLL 中的value值会被Hash函数计算得到一个 64bit 的值，低14位用于分桶，所以桶数为 $m=2^{14}=16384$ 个，高50位用于伯努利试验，需要6bit来存储 ($2^6=64>50$)。所以在Redis中，HLL仅用空间 16384 * 6bit = 12KB ，就可以统计多达 $2^{64}$ 个数。

算法的实现本身并不复杂，但是Redis还是对其内存占用作了一些优化。我们可以看出，无论基数多大，桶数都是16384个，所占用的内存都是12KB，当基数比较小时，还是会造成一些空间浪费。所以Redis采用稀疏存储结构和密集存储结构两种方式。

密集存储结构

密集存储结构类似于位图，是一个大小固定为12KB的数组，每6bit表示一个桶，存储该桶的$k_{max}$值，共计16384个桶，对每个桶的读写操作时，都需要一定的位运算，定位到桶的那6个比特并进行读写。密集存储结构如下图所示：

image-20210827005035494

稀疏存储结构

稀疏存储结构并不真的使用12KB的数组来表示16384个桶，而是使用特殊的字节结构来表达，如下图所示：

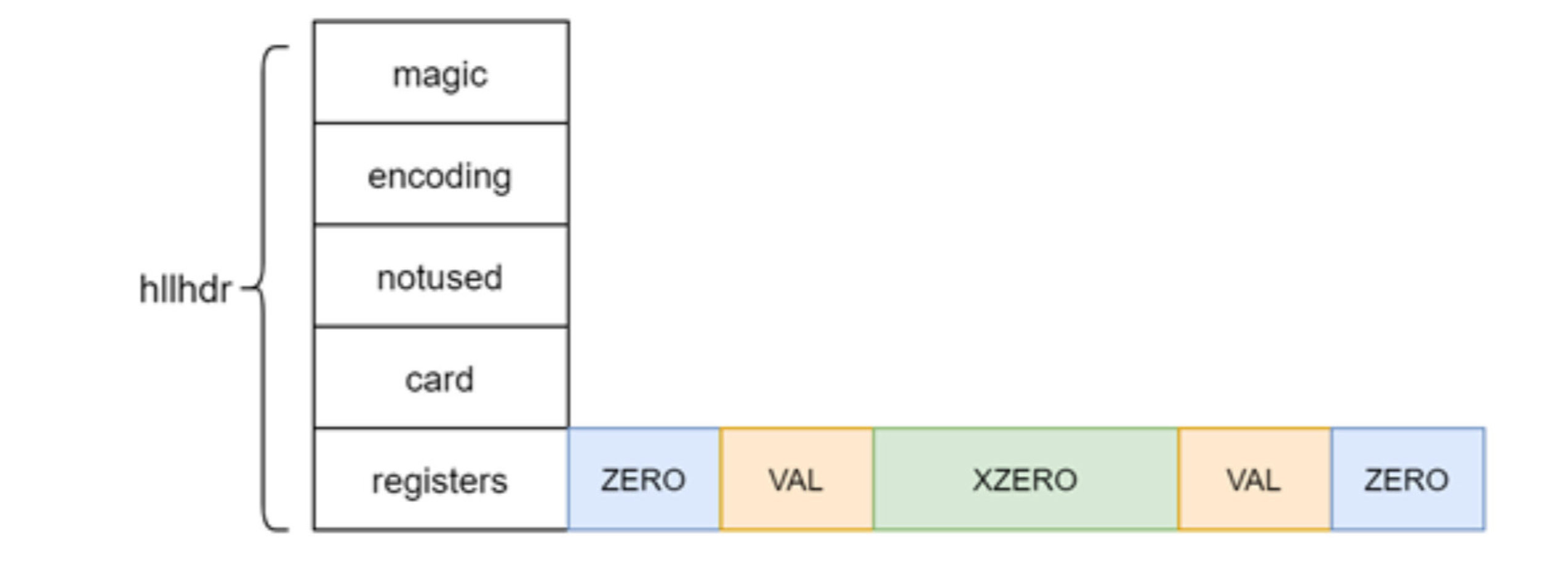
image-20210827005122167

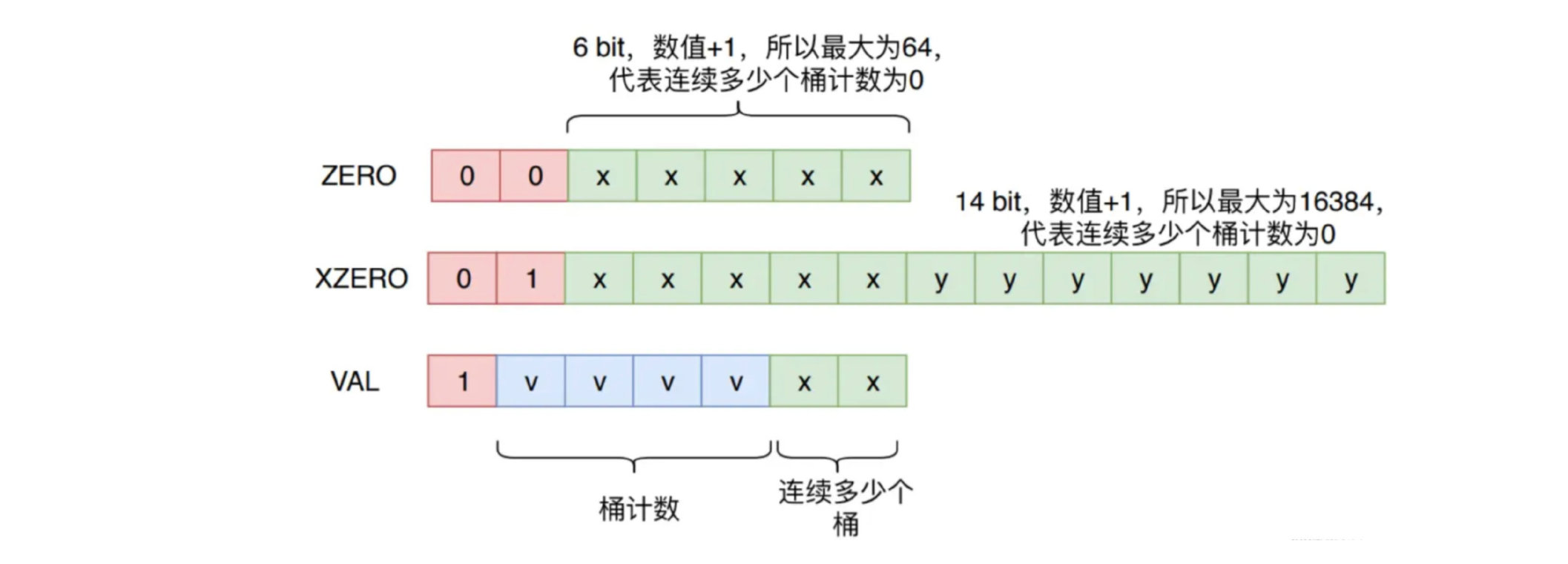
  • ZERO：占用1个字节，表示连续多少个桶的计数都是0。前2位固定是00，后6位表示有多少个桶，最大为64
  • XZERO：占用2个字节，表示连续多少个桶的计数都是0。前2位固定是01，后14位表示有多少个桶，最大为16384
  • VAL：占用1个字节，表示连续多少个桶的计数为多少。前1位固定是1，接下来5位表示计数的值是多少，所以最大是32。最后2位表示连续多少个桶

image-20210827005155548

所以，一个初始状态的 HyperLogLog 对象只需要2 字节，也就是一个 XZERO 来存储其数据，而不需要消耗12K 内存。当 HyperLogLog 插入了少数元素时，可以只使用少量的 XZERO、VAL 和 ZERO 进行表示，如下图所示。

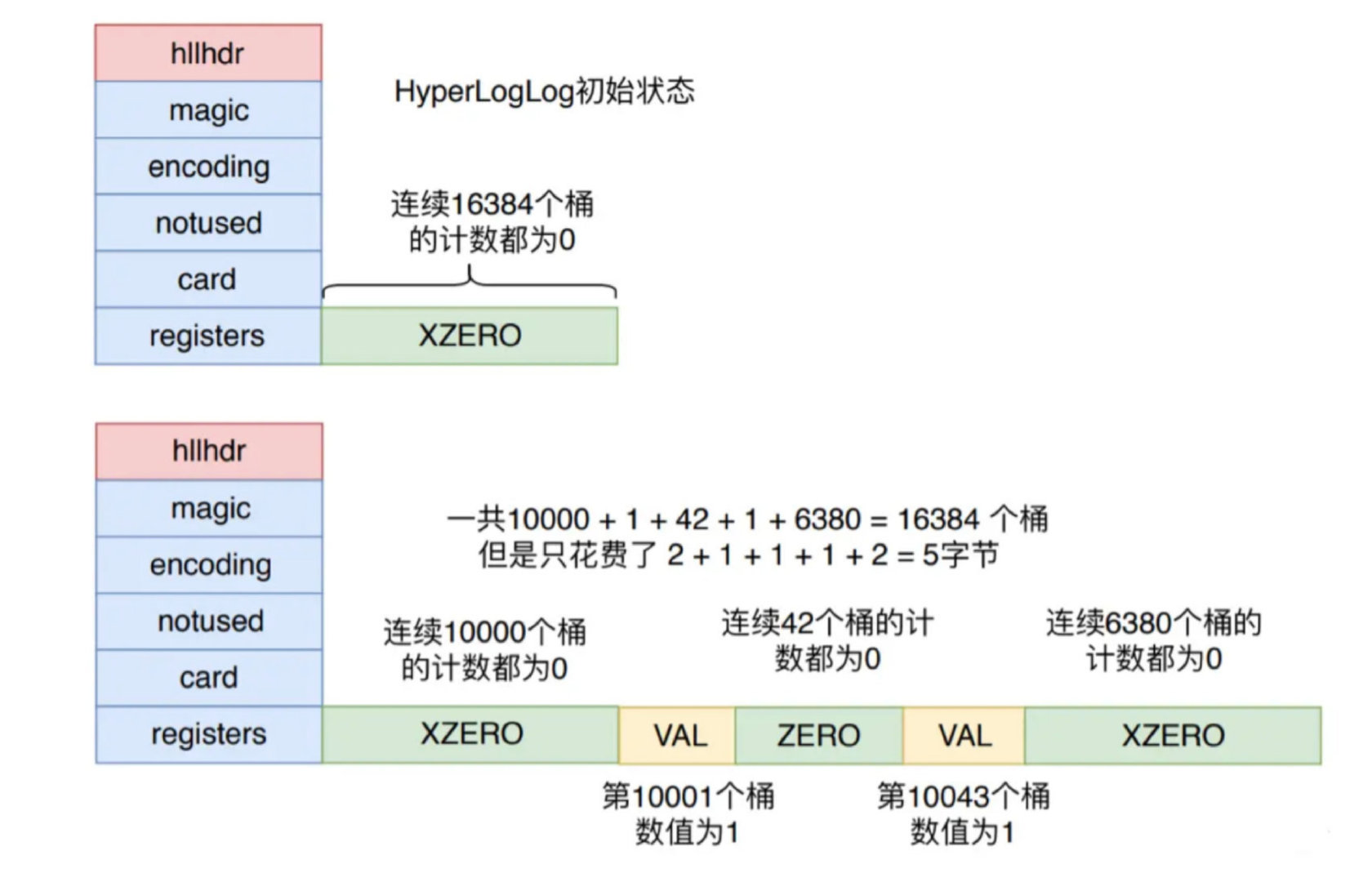
image-20210827005216323

Redis从稀疏存储转换到密集存储的条件是：

  • 任意一个计数值从 32 变成 33，因为 VAL 指令已经无法容纳，它能表示的计数值最大为 32
  • 稀疏存储占用的总字节数超过 3000 字节，这个阈值可以通过 hll_sparse_max_bytes 参数进行调整。

总结

本文介绍了HyperLogLog的相关命令以及基本原理，命令包括：

  • PFADD：添加元素
  • PFCOUNT：查询基数
  • PFMERGE：合并多个HyperLogLog

相关原理：伯努利实验、分桶优化、Redis实现

同时给大家推荐一个网站，可以可视化的看到HyperLogLog的变化过程： HyperLogLog 工具网址

更多

微信公众号：CodePlayer

参考文档